An interval in music is the pitch difference between two sounds, serving as the foundational element that shapes melodies, harmonies, and chords. Understanding what are musical intervals is crucial for creating, analyzing, and appreciating music effectively.
Introduction
What’s a musical interval? Picture yourself sitting at a piano. You strike two keys, either simultaneously or one after the other. The pitch difference, or the “gap” between those sounds, is a musical interval. Simply put, musical intervals are the steps in the musical staircase connecting different pitches.
Why are these steps so crucial? Just as bricks form the foundation of a building, intervals act as the primary components of music. They construct the melodies, harmonies, chords, and even intricate chord progressions. They are the constituents that mold the tonal landscape of a piece of music.
The knowledge of musical intervals is a powerful tool:
- It equips you with the capacity to analyze and construct music. It is fundamental to understanding how musical scales are built, as scales are essentially a sequence of specific intervals.
- It unlocks the mystery behind the allure of certain melodies, the expressive power of chord progressions, and the art of utilizing these elements in your compositions.
- A solid grasp of intervals provides the essential musical vocabulary to collaborate effectively with other musicians. Moreover, it enhances your ability to play music by ear.
This article is designed to be your comprehensive guide, delving into musical intervals’ intricacies and exploring their classifications, characteristics, and practical applications. It’s structured to cater to music enthusiasts at all levels.
The Basics of Musical Intervals
Let’s dive into the fundamental building blocks of music: musical intervals. They are a core concept underpinning melody, harmony, and virtually all musical structures.
Definition of Interval in Music
At its most basic, a musical interval represents the distance between two pitches in music. It is the primary building block that creates the familiar melodies and harmonies we hear in music. Think of it as a bridge connecting two musical notes.
This distance between pitches is typically measured in whole and half steps. If you’re unfamiliar with the concept of whole and half steps, I recommend reading our previous article about this topic.
If you strike two keys on a piano in sequence or simultaneously, the musical interval is the pitch difference between those two notes, measured in whole and half steps. This difference is quantified in a specific way in music theory, a system we’re about to delve into.
Musical intervals refer to sequential pitches (melodically) and simultaneous pitches (harmonically). When two notes are played one after the other, it’s called a melodic interval. Conversely, when the two notes are played simultaneously, it’s called a harmonic interval.
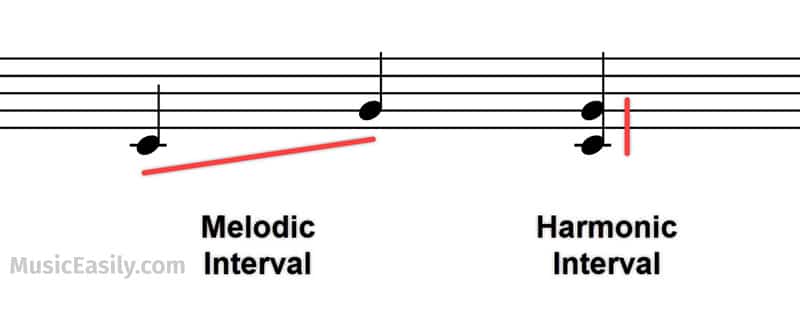

The Role of Intervals in Melody and Harmony
Consider musical intervals as the lifeblood of melodies and harmonies.
In a melody – the catchy tune you can’t get out of your head – musical intervals are the steps you take from one note to another. These steps form that unique pattern that gives a melody its identifiable character.
Harmony, in contrast, often involves playing several intervals concurrently, resulting in chords. The specific musical intervals within a chord determine its unique tonal quality.
Whether in a melody’s linear progression or harmony’s simultaneous sounds, intervals play a fundamental role. But the importance of understanding intervals isn’t confined to theory—it’s a practical skill for composers and songwriters.
Naming Musical Intervals
In music, we have a specialized language to express the distance between notes. Rather than referring to one note as “higher” or “lower,” we give a specific name to the interval separating them.
An interval name is made up of two elements: a numerical value (unison, second, third, etc.) and a “quality” descriptor (perfect, major, minor, augmented, or diminished).
- The numerical component of the interval name correlates with the count of letter names it includes, regardless of any accidentals (sharp or flat modifications) on either note. For instance, the interval from A to C (whether A#, A, or Ab to C#, C, or Cb) always covers three letter names (A, B, C), making it a third. Similarly, the interval from C to G (whether C#, C, or Cb to G#, G, or Gb) spans five letter names (C, D, E, F, G); therefore, it’s a fifth.
- The quality of the interval (major, minor, perfect, augmented, or diminished) is determined by the exact number of half steps within that interval. For example, a major third includes four half-steps, and a perfect fifth comprises seven half-steps.
Combining these two aspects, we create a comprehensive language to describe intervals. For instance, the distance from C to Eb, encompassing three letter names (C, D, E) and three half-steps, is identified as a “minor third.” Similarly, the gap from C to G, spanning five letter names (C, D, E, F, G) and encompassing seven half-steps, is known as a “perfect fifth.”
This dual-component system specifies the exact distance between the two pitches, and implies the harmonic and tonal relationship, offering a more holistic understanding of the musical interval.
Now that we explored the fundamental structure of interval naming, our next step is to delve deeper into this concept. The following section will comprehensively analyze the numerical values used in naming musical intervals, aiding our understanding of these distances on a staff or keyboard.
The Numerical Component of Musical Intervals
With a firm understanding of how we name intervals and the integral role of numerical values, let’s explore these intervals to enhance our comprehension further. The numerical part of an interval’s name is straightforward—yet crucial—for understanding the relative distance between notes on a staff or keyboard.
Unison
Unison, as a type of interval, most commonly occurs in a harmonic context.
Harmonically, unison occurs when two notes of the same pitch are played simultaneously. A guitar could achieve this by simultaneously playing the same note on two strings at different frets.
In an orchestral or ensemble setting, unison could occur in various ways. It might involve two instruments, like a flute and a violin, simultaneously playing the same note. Alternatively, it could be two violins — played by separate musicians — playing the same note simultaneously. This simultaneous sounding of the same pitch can add depth and richness to a performance.
Let’s explore the concept of unison through an auditory example, where an ensemble of string instruments harmoniously produces the same note simultaneously, a perfect illustration of harmonic unison.
Second
A second spans two note names, regardless of accidentals. On a keyboard, a second is the distance from one key to the first key that has a different letter name. For example, from C to D, C to D#, or even C to Db. In these cases, while the interval’s quality may change based on the exact number of half steps, the numerical value remains a second because the letter names differ.

Third
A third spans three note names, regardless of accidentals. On a keyboard, a third is the distance from one key to the second key that has a different letter name. For example, from C to E, C to E#, or C to Eb.

Fourth
A fourth spans four note names, regardless of accidentals. On a keyboard, a fourth is the distance from one key to the third key that has a different letter name. For example, from C to F, C to F#, or C to Fb.

Fifth
A fifth spans five note names, regardless of accidentals. On a keyboard, a fifth is the distance from one key to the fourth key that has a different letter name. For example, from C to G, C to G#, or C to Gb.

Sixth
A sixth spans six note names, regardless of accidentals. On a keyboard, a sixth is the distance from one key to the fifth key that has a different letter name. For example, from C to A, C to A#, or C to Ab.

Seventh
A seventh spans seven note names, regardless of accidentals. On a keyboard, a seventh is the distance from one key to the sixth key that has a different letter name. For example, from C to B, C to B#, or even C to Bb.

Octave
An octave, also known as an 8th, is a specific type of interval in music that spans eight note names, reaching the same letter note (including the same accidentals, if any) in the next higher or lower register.
For example, it’s the distance from one note, like C, to the next higher or lower C, from C# to the next higher or lower C#, or from Cb to the next higher or lower Cb. On a keyboard, this would be the distance from one key to the next key, an octave away that shares the same letter name and accidentals.
The term octave specifically refers to the interval where the frequency ratio is 2:1. If the interval is altered by a change in accidentals (like going from C to C# or C to Cb an octave higher), the interval is no longer considered an octave. In this context, an octave is synonymous with a “perfect octave,” as it changes the pitch, and the frequency ratio isn’t exactly 2:1.
These altered intervals are known as an augmented or diminished octave, respectively.
The Qualities of Musical Intervals
Now that we’ve delved into the numerical component of musical intervals—understanding terms like 2nd, 3rd, octave, and so forth—it’s time to delve deeper and explore the distinct qualities of these intervals.
Perfect, major, minor, diminished, and augmented qualities further define each interval. They contribute to the unique sound of each interval and play a vital role in shaping the overall tonal expression of a piece of music.
Perfect Intervals
Let’s start with perfect intervals. This group includes the unison, fourth, fifth, and octave. They earn the “perfect” label due to their clear, consonant sound and fundamental role in harmony and melody.
These intervals sound so well connected because their frequencies are intimately related. The frequency ratios for a perfect octave, fifth, and fourth are 2:1, 3:2, and 4:3, respectively. In contrast, other intervals like major and minor thirds have more complex ratios, making them less perfect.
Their presence brings a sense of equilibrium and resolution, making them central to our musical perception. When these intervals are altered, they often create a sense of dissonance, signaling a departure from musical norms.
| Interval | Number of Half Steps | Numerical Name for Interval |
|---|---|---|
| Unison | 0 | 1st |
| Perfect forth | 5 | 4th |
| Perfect fifth | 7 | 5th |
| Octave | 12 | 8th |
For a visual illustration of how perfect fifths (or fourths) relate to each other across different keys, check out our post on the Circle of Fifths.
Major and Minor Intervals
Following the perfect intervals, we have the major and minor intervals. The major intervals are often associated with a cheerful, bright sound, while minor intervals bring a more somber, reflective mood.
These include the seconds, thirds, sixths, and sevenths. They are key players in setting the emotional tone of a song.
The distinction between a major and a minor interval is defined by the number of half steps it comprises. For example, a major third consists of four semitones, while a minor third consists of three.
This slight shift in size dramatically changes the tonal color and emotional impact of the interval.
| Interval | Number of Half Steps | Numerical Name for Interval |
|---|---|---|
| Minor second | 1 | 2nd |
| Major second | 2 | 2nd |
| Minor third | 3 | 3rd |
| Major third | 4 | 3rd |
| Minor sixth | 8 | 6th |
| Major sixth | 9 | 6th |
| Minor seventh | 10 | 7th |
| Major seventh | 11 | 7th |
Diminished and Augmented Intervals
Finally, we encounter diminished and augmented intervals. While they are not as common as the others, they play a vital role in more complex harmonic structures.
A diminished interval is a half step smaller than a perfect or minor interval. Conversely, an augmented interval is a half step larger than a perfect or major interval.
These adjustments introduce a sense of tension or discord, which can be utilized creatively to generate musical interest or to guide a progression toward a resolution.
These intervals are often featured in musical styles that exploit tension and resolution, such as jazz, blues, and classical compositions.
The following table shows the most common diminished intervals.
| Interval | Number of Half Steps | Numerical Name for Interval |
|---|---|---|
| Diminished fourth | 4 | 4th |
| Diminished fifth | 6 | 5th |
The following table shows the most common augmented intervals.
| Interval | Number of Half Steps | Numerical Name for Interval |
|---|---|---|
| Augmented second | 3 | 2nd |
| Augmented fourth | 6 | 4th |
| Augmented fifth | 8 | 5th |
Formatting and Abbreviation of Musical Intervals
When it comes to writing these interval names, we use a specific system that’s consistent across musical literature. The quality descriptor is always written in lowercase. In contrast, when feasible for readability and simplicity, the numerical value is written in lowercase and as a numeral.
For instance, a “major sixth” interval would be written as “major6“. Similarly, a “diminished fifth” could be written as “diminished5“.
Another example could be a “minor second”, written as “minor2“. An “augmented fourth,” on the other hand, would be written as “augmented4“.
Each quality descriptor also has a widely accepted abbreviation. For example, “major” is often abbreviated as “M,” “minor” as “m,” “perfect” as “P,” “augmented” as “Aug” or “A,” and “diminished” as “dim” or “d.” The numerical values aren’t abbreviated due to their already short length.
Now, let’s see how these rules work with examples. A “major third,” which covers three letter names and includes four half-steps, is written as “M3“. Similarly, a “minor third,” covering three letter names but with only three half-steps, is denoted as “m3“.
A “perfect fifth,” spanning five letter names and seven half-steps, is written as “P5“. When it comes to augmented or diminished intervals, we can write an “augmented fourth” as “Aug4” or “A4” and a “diminished seventh” as “dim7” or “d7“.
Using this method of writing musical intervals, we can consistently and concisely communicate the specific pitch relationships within a piece of music.
| Quality | Abbreviation | Example |
|---|---|---|
| diminished | dim (or “d”) | d4 |
| minor | m | m2 |
| perfect | P | P5 |
| major | M | M3 |
| augmented | Aug (or “A”) | A5 |
Types of Musical Intervals
Not all musical intervals are identical. They vary in size and character, each with its characteristics and uses in music. There are two primary classifications of intervals in music: simple and compound. Let’s explore each one in detail.
Simple Intervals
Consider simple intervals as the foundational building blocks of music. These are intervals that span an octave or less. They’re the raw materials from which we construct all other intervals. The roster of simple intervals includes unisons (the same note duplicated), seconds, thirds, fourths, fifths, sixths, sevenths, and octaves.
Each of these simple intervals contributes a distinct signature to music. For example, unisons and octaves, known as “perfect” intervals, contain notes of the same pitch class. Similarly, perfect fourths and fifths provide a sense of harmonic balance.
The remaining simple intervals – seconds, thirds, sixths, and sevenths – can be either major or minor, adding a richer, more nuanced tonal palette crucial for crafting compelling melodies and harmonies.

Compound Intervals
When we venture beyond the one-octave mark, we encounter compound intervals. These intervals exceed the span of an octave and include ninths, tenths, and so forth.
There’s a fascinating correlation between compound and simple intervals. You can think of a compound interval as a simple interval supersized by adding one or more octaves.
For example, consider a major tenth. This interval spans two staff positions above one octave. But what is it in simpler terms? It’s one octave plus a major third. Hence, it can also be called a “compound major third.”
So why two names? The first name, “major tenth,” reflects the exact distance between the two notes, both in terms of pitch and on the staff. The second name, “compound major third,” tells us the basic quality and type of the interval, disregarding the extra octaves.
The following table provides an overview of how we can label these larger intervals that exceed an octave. By understanding these different naming conventions, you can better understand how compound intervals function within a piece of music.
| Simple Interval + Octave | Numerical Name for Interval | Interval Name Using Octave |
|---|---|---|
| 2nd + 1 octave | 9th | Compound 2nd |
| 3rd + 1 octave | 10th | Compound 3rd |
| 4th + 1 octave | 11th | Compound 4th |
| 5th + 1 octave | 12th | Compound 5th |
| 6th + 1 octave | 13th | Compound 6th |
| 7th + 1 octave | 14th | Compound 7th |
Even though compound intervals are larger, they often preserve some sonic traits of their corresponding simple intervals but with an added sense of spaciousness and scope.
This attribute makes compound intervals particularly valuable in musical settings with a desired broader pitch range, such as orchestration or arrangement.
Inversions of Musical Intervals
The concept of interval inversions is an integral part of understanding music theory. Inverting an interval involves flipping it upside down – taking the lower note and moving it above the higher note or vice versa.
This versatile tool can greatly enhance the richness of your musical compositions and arrangements.
Understanding Inverted Intervals
First off, let’s clarify what an inverted interval is. You create an inverted interval by taking any two notes that form an interval and swapping their positions.
For instance, if you have a C and an E, with C being the lower note, you’d invert the interval by shifting the C to above the E.
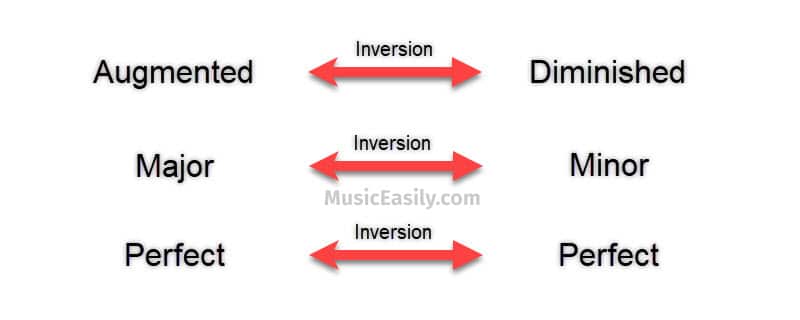
In terms of their quality, inverted intervals have some interesting characteristics. Major intervals become minor when inverted, and minor intervals become major. Perfect intervals remain perfect, and diminished intervals become augmented (and vice versa).
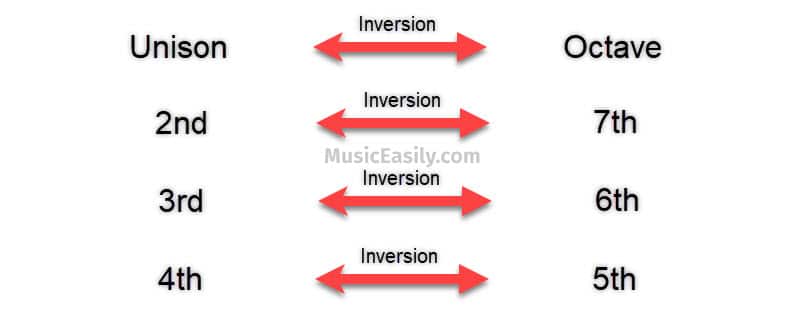
Besides the quality, the numerical size of the interval also transforms when inverted. The numeric inversion rule is quite straightforward. An interval and its inversion always add up to nine.
For example, if you invert a second, you get a seventh (2 + 7 = 9); if you invert a third, you get a sixth (3 + 6 = 9). Similarly, inverting a fourth gives you a fifth (4 + 5 = 9), and vice versa. When it comes to unisons and octaves, they invert into each other, maintaining the sum of nine (1 + 8 = 9).
So, whether it’s quality or numeric size, inverted intervals reveal fascinating dynamics underpinning musical harmony.
Practical Uses of Inverted Intervals
The theory behind inverted intervals isn’t merely academic; it has substantial practical implications in music composition, arrangement, and songwriting.
In melody writing, inverted intervals can provide an interesting variation of a melodic theme. You can create a melody that feels familiar yet different by inverting the intervals.
In harmony, inverted intervals can generate alternative “chord voicings.” A chord voicing describes the specific arrangement of the notes within a chord. In a conventional triad chord (a chord comprising three notes), you encounter a root, a third, and a fifth.
Take, for example, a C major chord, which consists of C (the root), E (the third), and G (the fifth). When we discuss “inverting a chord,” we mean altering the order of these notes.
In a C major chord, if we take the root note (C in this instance) and transpose it an octave higher, the chord now starts with E (the third), followed by G (the fifth), and finally C (the root, now transposed an octave higher). This results in a sequence of E-G-C called a “first inversion” chord.
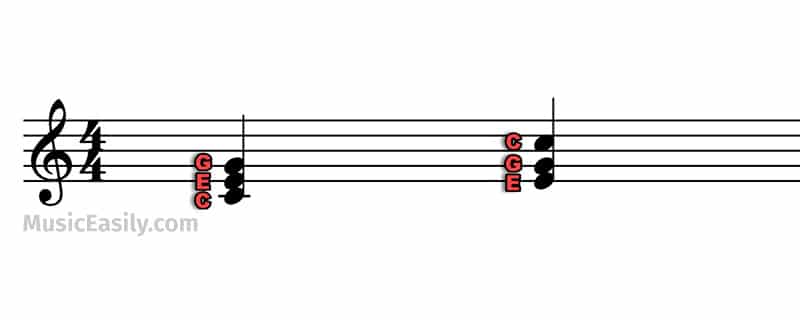
The effect of this inversion is a nuanced shift in the sound or “tonal color” of the chord. This can contribute to more dynamic and smoother transitions, known as “voice leading,” between chords within a progression.
As for arrangements, you can leverage inverted intervals to distribute the notes of a chord across various instruments. This technique helps achieve a well-rounded and effective orchestration.
In essence, mastering the concept and application of inverted intervals can equip you with additional creative strategies for your music.
Conclusion
Understanding musical intervals is more than just an academic exercise for those interested in music.
From the basic building blocks of simple intervals through the expressive qualities of perfect, major, minor, diminished, and augmented intervals, each has a role in the soundscape of a piece of music. They define the character of melodies, harmonies, and chord progressions, influencing our emotional response to music.
Their practical application is evident in songwriting, where understanding intervals can enhance the creative process, allowing you to craft tunes that evoke specific emotional responses.
To delve deeper into the fascinating world of musical intervals, you might find this Wikipedia article (ext. link) useful.


